Quantum Computing: The use cases for the future of computing

The technology of quantum computing has seen a significant influx of capital in the past couple of years, increasing from $93.5m in 2015 to $3.2bn in 2021, with VC and private capital making up more than 70% of investments. Even though this year has been a more or less quit year for VCs so far, there are some big investments that are worth to be mentioned. Israeli startup Quantum Machines announced earlier this month a $20 million extension to the $50 million Series B round it raised last September. Similar announcements this month came from Paris-based quantum computing startup PASQAL which has raised €100 million in a Series B funding round and UK-based Oxford Ionics which has raised £30 million in Series A funding.

However, the majority of funding does not come from private entities. Quantum research and consulting firm GQI, tracking government-funded projects by agencies and institutes in a number of countries, reported a total of more than $55 billion in state-sponsored research and development initiatives worldwide. The report also notes that most quantum technology patents are filed by companies in China (54%) and Japan (15%) and that there are currently 162 universities and institutions worldwide with quantum-information-science-focused educational programs and research activity. To get a better picture of the worldwide governmental programs, please take a look at the following landscape graphic:

Navigating the intricate web of the financial world can be a daunting task, with its labyrinth of interconnected systems, colossal data volumes, and the ceaseless requirement for prompt, accurate calculations. Quantum computing, with its unparalleled computational prowess, stands poised to overhaul how we steer this vast financial ocean. Let’s dive deeper to explore the potential of quantum computing to transform two cornerstone elements of finance: 1) risk evaluation and portfolio optimization, along with 2) real-time trading.

Risk assessment and portfolio optimization

Risk evaluation teamed with portfolio optimization lies at the heart of all successful financial strategies. This process involves exploring myriad combinations of investments, aiming to strike an optimal balance between risk and return. However, as the number of assets balloons, this quickly escalates into an exponentially challenging problem for conventional computers.

This is where quantum computing strides in. Thanks to their ability to tap into the principles of superposition and entanglement, quantum computers can handle colossal data amounts concurrently. This makes them uniquely suited to tackle such complex problems. Quantum algorithms, like the Quantum Approximate Optimization Algorithm (QAOA), are capable of traversing the multifaceted landscape of financial data more efficiently. They can identify optimal portfolios in a fraction of the time taken by traditional algorithms.

Building an optimal portfolio with a quantum computer relies on the use of exactly these QAOAs. The goal is to find the optimal combination of assets that maximizes return and minimizes risk, a task that is remarkably complex given the vast number of potential asset combinations and the probabilistic nature of returns and risks.

Here’s a simplified description of how it works:

1. Each potential portfolio is represented as a quantum state. A quantum computer, with its qubits, can hold a superposition of these states, effectively considering all possible portfolios at once due to the principle of superposition.
2. Each potential portfolio is assigned a cost based on a predetermined cost function, which might reflect the overall risk of the portfolio or some other measure of undesirability.
3. The quantum algorithm attempts to minimize this cost function. This is done by applying a series of quantum operations (also known as gates) to manipulate the state of the qubits. These gates are applied repeatedly in an iterative process, each time nudging the system a little closer to the state representing the optimal portfolio.
4. Quantum interference is leveraged to amplify the probability of the optimal portfolio and reduce the probability of less desirable portfolios. This is where the inherent probabilistic nature of quantum computing comes into play.
5. After a number of iterations, the quantum state is measured, collapsing the superposition of states down to a single state due to the quantum mechanical principle of measurement. With a well-tuned algorithm, this state should correspond to the optimal portfolio with high probability.
6. The quantum computer then provides the optimal portfolio as output, which can be used to make informed investment decisions.

This method surpasses traditional computer algorithms that usually have to test each portfolio combination sequentially, which can be computationally intensive and time-consuming for large sets of assets.

Obviously, this is a simplification and actual implementation involves more complex quantum mechanics. Also, while this process holds great potential, it is still a topic of ongoing research and has not yet been fully realized in practice due to the current technological constraints of quantum computers. Especially the cost and complexity of operating such a system make it nearly impossible to use it at scale for these cases.

Additionally, quantum computing can substantially boost Monte Carlo simulations, which are widely used in finance for risk evaluation. Monte Carlo methods use random sampling to estimate numerical quantities which are hard to compute deterministically. While they are robust tools, they can also be computationally demanding and slow on conventional computers. In really simple terms, a Monte Carlo simulation creates a distribution curve through an interactive process of previous simulations which can be seen in the graphic below:

Monte Carlo simulations are often used in the valuation of options and portfolio valuation. The prices of an underlying share are simulated for each possible price path, and the option payoffs are determined for each path. The option price is then the average of the paths discounted to today. For portfolio valuation, a Monte Carlo simulation models all the factors influencing the price of the portfolio. Then the average value of all simulations is observed, which provides the average value of the overall portfolio. The output then is exactly this density function, displaying the most likely prices and the value distribution around the average.

Quantum computers, with their superior processing capabilities, can execute these simulations more rapidly and accurately, leading to more dependable risk evaluations. A study published at the Royal Society in 2015 argues that the usage of quantum computing can reduce the calculations in a quadratic time dependent on the number of simulations needed. At the core of this advancement are quantum walks. Basically, these are random walks on finite graphs generalized to the quantum world. They do not converge to any stationary distribution, as they are unitary and reversible, which is why the calculation times compared to normal random walks are quadratically faster.

Trading and pricing of assets

The financial markets resemble a relentless maelstrom of activity, with countless transactions unfolding every second. This high-speed environment necessitates equally rapid and precise decision-making—a challenge that quantum computing is perfectly positioned to tackle.

Traditional algorithms often stumble when trying to keep up with real-time market data, resulting in delayed decision-making and lost opportunities. Quantum computers, on the other hand, can process and analyze real-time data swiftly, facilitating faster, more informed trading decisions. This is not only limited to trading directly. But with the increased amount of data that quantum computers can use simultaneously, the pricing of assets can potentially see far more advanced techniques being used in the future.

Quantum computers can help overcome the ‘curse of dimensionality‘ that often plagues financial modeling. This phenomenon refers to the exponential spike in computational complexity as the number of variables in a model multiplies. In options pricing, for instance, a plethora of variables need to be accounted for — asset price, strike price, time to expiration, interest rates, and volatility. Quantum computers can manage this high-dimensional data more efficiently than their classical counterparts, enhancing the speed and accuracy of financial models. Tristan Fletcher, Co-founder of an AI forecasting company called ChAI said that the usage of quantum computing is more likely in solving difficult problems instead of leveraging the quickness of these calculations for real-time trading directly. His quote underlines quite nice of how advanced supercomputers already are in real-time trading. “We are already at the limits of what any system that isn’t actually listening to Opec meetings and five-year plans is capable of”.

While the integration of quantum computing into the financial sector is still in its infancy, and challenges persist, the potential benefits it promises—enhanced risk assessments, optimized portfolios, and trading and pricing capabilities—paint a promising future.

Quantum computing holds both a significant promise and a potential threat to the world of cryptography and cybersecurity. This dual nature lies in its capacity to vastly improve security measures, but also its potential to break existing encryption standards. Now, let’s delve into these aspects, starting with Quantum Key Distribution.

Quantum key distribution

Quantum Key Distribution (QKD) is a cutting-edge cryptographic procedure that allows the secure sharing of encryption keys between two parties. At the heart of this procedure is the sharing of encoded information across a quantum channel. Intriguingly, due to the intrinsic peculiarities of quantum mechanics, any attempted interception or measurement of the data triggers an irreversible transformation in its state. The recipients can detect this anomaly, thereby exposing the snoop.

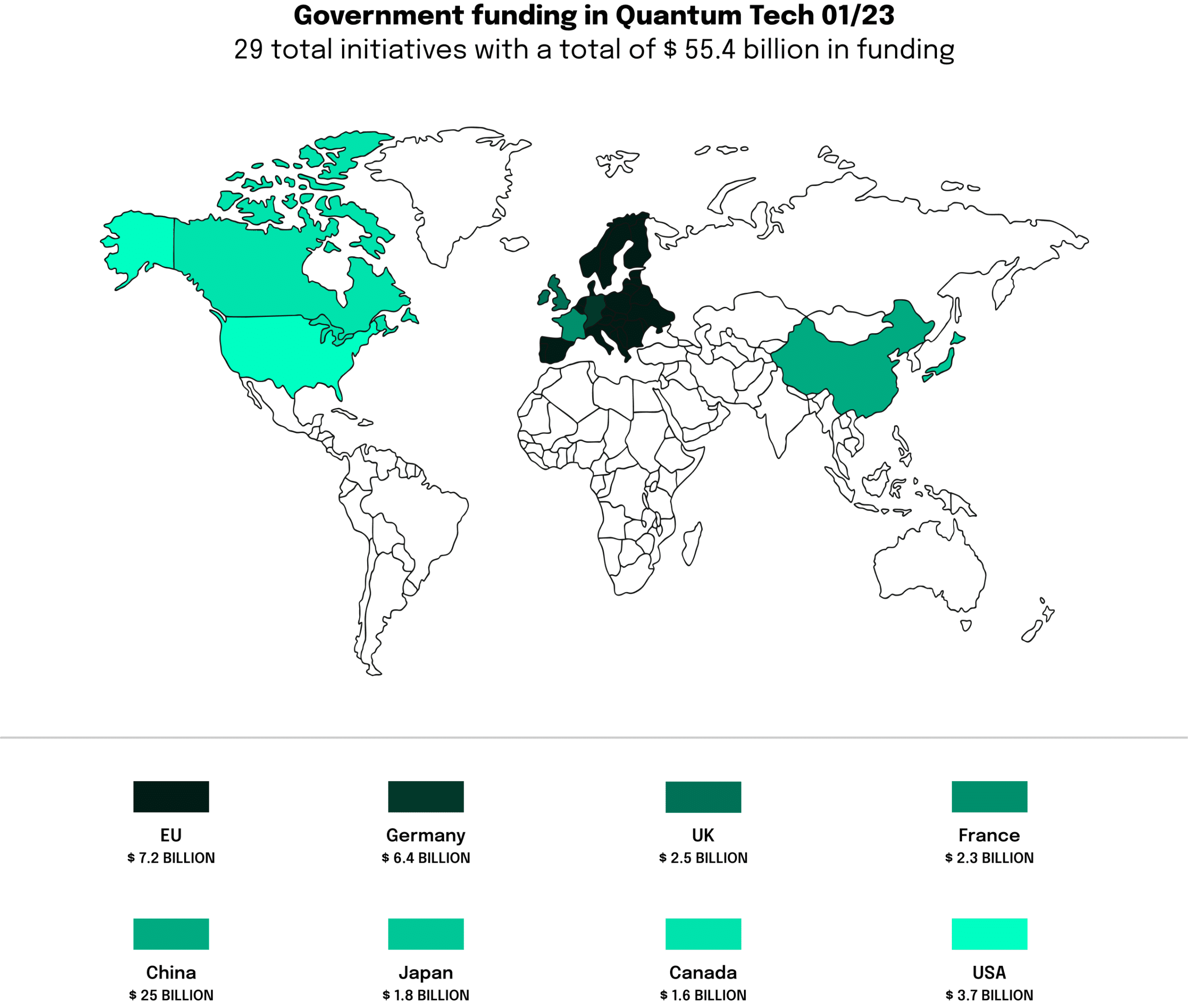
QKD’s defining characteristic is its theoretical invincibility against interception, making it a formidable weapon in the arsenal of next-generation cybersecurity. Several nations, China being a notable example, have begun utilizing QKD for safeguarding high-stakes communication channels, thereby showcasing the practical utility of quantum concepts in cryptography.

Breaking classical cryptography

Conversely, quantum computers are a looming storm cloud over classical cryptography. Algorithms devised for quantum computing, such as Shor’s algorithm, have the potential to decipher the widespread RSA encryption in polynomial time – a feat that poses an insurmountable challenge to classical computers. The fallout of this could be the exposure of a substantial volume of encrypted global data.

Modern encryption protocols, for instance, RSA and ECC, rest upon the computational difficulty of factoring large numbers or pinpointing discrete logarithms. Multiplying two numbers by each other can be solved with pencil and paper in any size. To decompose the same number into its prime factors, with today’s possibilities of mathematics, works in fact only by approximation and then trial and error. By efficiently factoring these numbers, Shor’s Algorithm could potentially break these encryption schemes.

These tasks are a tall order for classical computers. However, quantum computers can accomplish these tasks efficiently, thereby casting a long shadow over current encryption practices. Consider a classical four-bit computer. Since classical bits can only be in one state at a time, these computers can only store 2^4=16 possibilities at the same time. That’s why it takes classical computers so long to divide numbers into prime factors as it is requested by RSA encryption. For a quantum computer other standards apply. A four qubits quantum computer, in superposition, is designed to be in all 16 possible combinations simultaneously. With this knowledge and Shor’s algorithm in mind, the quantum computer can store over one million values simultaneously (2^20 = 1,048,576). A big challenge for keeping information secure with classical methods.

This is not to suggest that the advent of quantum computers will lead to an overnight compromise of all security systems. The hardware prerequisites for running such algorithms on quantum computers are still far off. However, it is an alarm bell that signifies the urgent need for post-quantum cryptography.

On one side, quantum computing offers the promise of revolutionizing secure communication, courtesy of techniques like QKD. On the other, it poses a looming threat to existing encryption practices and underscores the urgency of evolving quantum-resistant algorithms. The discipline of cryptography is merely one among the plethora where the quantum revolution will usher in profound shifts, giving rise to novel opportunities and hurdles alike.

The expansive scope of quantum computing encircles even the most exigent problems of our era, a prime example being the persistent climate crisis. With the intricate web of factors involved and the substantial volume of data to analyze, climate studies and forging effective ecological solutions are formidable tasks. Yet, quantum computing brings forth the potential for substantial strides in these sectors.

Enhancing climate models

The process of climate projection necessitates the simulation of complex interconnected systems, encompassing elements like atmospheric patterns, oceanic currents, and biological ecosystems. For accurate predictions of climate alterations and an understanding of the plausible effects, we must manage an extensive series of variables and anticipate their interactions—an undertaking fitting for quantum computers.

Quantum computers, with their intrinsic capacity for concurrent processing and analysis of massive datasets, could revolutionize climate projection. Their ability to manage intricate simulations that currently outstrip the capabilities of traditional computers could lead to more precise climate predictions. This granular understanding of climate trends is essential for informed decision-making in climate policy and strategic planning.

Catalyzing eco-friendly technologies

Quantum computing could also serve as a catalyst in the evolution of green technologies. It opens up novel avenues toward materials and processes that are more energy-efficient. For instance, quantum computers could aid in devising superior solar cells by simulating various materials and setups to maximize efficiency. The principle on which solar cells operate, the photovoltaic effect, is fundamentally a quantum mechanical process.

Therefore, simulating this process on a quantum computer could potentially yield a level of accuracy that surpasses what classical computers can currently achieve. These simulations can be conducted using algorithms like the Variational Quantum Eigensolver (VQE). VQE can deduce the lowest energy state of a molecule, a critical property when anticipating how that molecule will react. By enabling a more precise simulation of various materials and configurations, researchers could unearth novel materials or structures that enhance the efficiency, longevity, or cost-effectiveness of solar cells. Simply put, quantum computing stands to elevate our capacity to develop advanced green technology, bolstering our arsenal in the global fight against climate change.

Quantum computing could potentially revolutionize the management and optimization of electrical grids. Imagine an electrical grid as a vast puzzle, one with countless variables that include power stations, transfer lines, and the fluctuating demands of consumers. Balancing the supply and demand in such a complex system, especially one with various renewable energy sources is an intricate optimization task that can perplex even the most powerful classical computers.

Diving deeper into the nuts and bolts, quantum algorithms like the Quantum Approximate Optimization Algorithm (QAOA) can unearth optimal solutions for convoluted systems. In relation to an electrical grid, a quantum computer running QAOA could devise the most efficient route to distribute power, reducing wastage and maximizing the grid’s operational efficiency. Besides the efficiency gains, quantum computing technology could also make our energy grids more secure and resilient to cybersecurity threats.

Quantum computing, while teeming with potential, is still in its infancy and faces a host of hurdles. Today’s quantum systems are error-prone and necessitate certain challenging-to-maintain conditions, such as ultra-chilled environments colder than outer space. They must also be expertly isolated to prevent external disruptions. As a result, quantum computers are delicate, with their quantum states easily disturbed by environmental noise.

In addition, the length of time during which qubits – the basic units of quantum information – can maintain their quantum state is extremely short. Often counted in microseconds, this limitation imposes a significant restriction on the duration and complexity of computational tasks. Programming quantum computers also presents a substantial challenge. Quantum algorithms require a sophisticated understanding of quantum physics and advanced mathematical concepts.

Finally, while Google’s proclamation of achieving “quantum supremacy” in 2019 made headlines, identifying practical problems where quantum computing can provide distinct advantages over classical computing is no small feat.

Despite these constraints, quantum computing’s revolutionary promise is undiminished. We’re seeing steady advancements in enhancing qubit stability, increasing coherence times, and developing robust quantum programming languages. These advancements are paving the way to more reliable and efficient quantum computing systems.

Predicting when fully functional, error-free quantum computers will be a reality is challenging, with estimates varying from ten to several decades. But there is a balance that can be found between classical computers and fully-functioning quantum computers. As real physical qubits, such as the state of trapped ions or electron spin, are subject to thermal, electromagnetic, and other interference to lead to computational errors, there are imperfect quantum computers already at work. Today’s imperfect quantum machines – referred to as Noisy Intermediate-Scale Quantum (NISQ) devices – may offer computational benefits for certain tasks and serve as useful testing grounds for quantum algorithms. In his paper from 2008, John Phillip Preskill stated that a quantum computer with a number of qubits of 50 to 100 can function better than today’s digital machines, even if they are fully exposed to the current level of environmental noise.

Although the full use of universal quantum computing in finance, climate research, and cryptography seems a difficult task, the potential of the technology is clear. However, less time spent on research and development of new ecological materials are also feasible. With increased computational speed, the impact of quantum computing on the financial industry, can revolutionize the way assets are valued and portfolios are assessed. One of the greatest potentials for innovation is in cryptography, where quantum computing represents both a threat and an opportunity for digital security! But other use cases in drug research and personalized medicine are also conceivable.